Hush 🇦
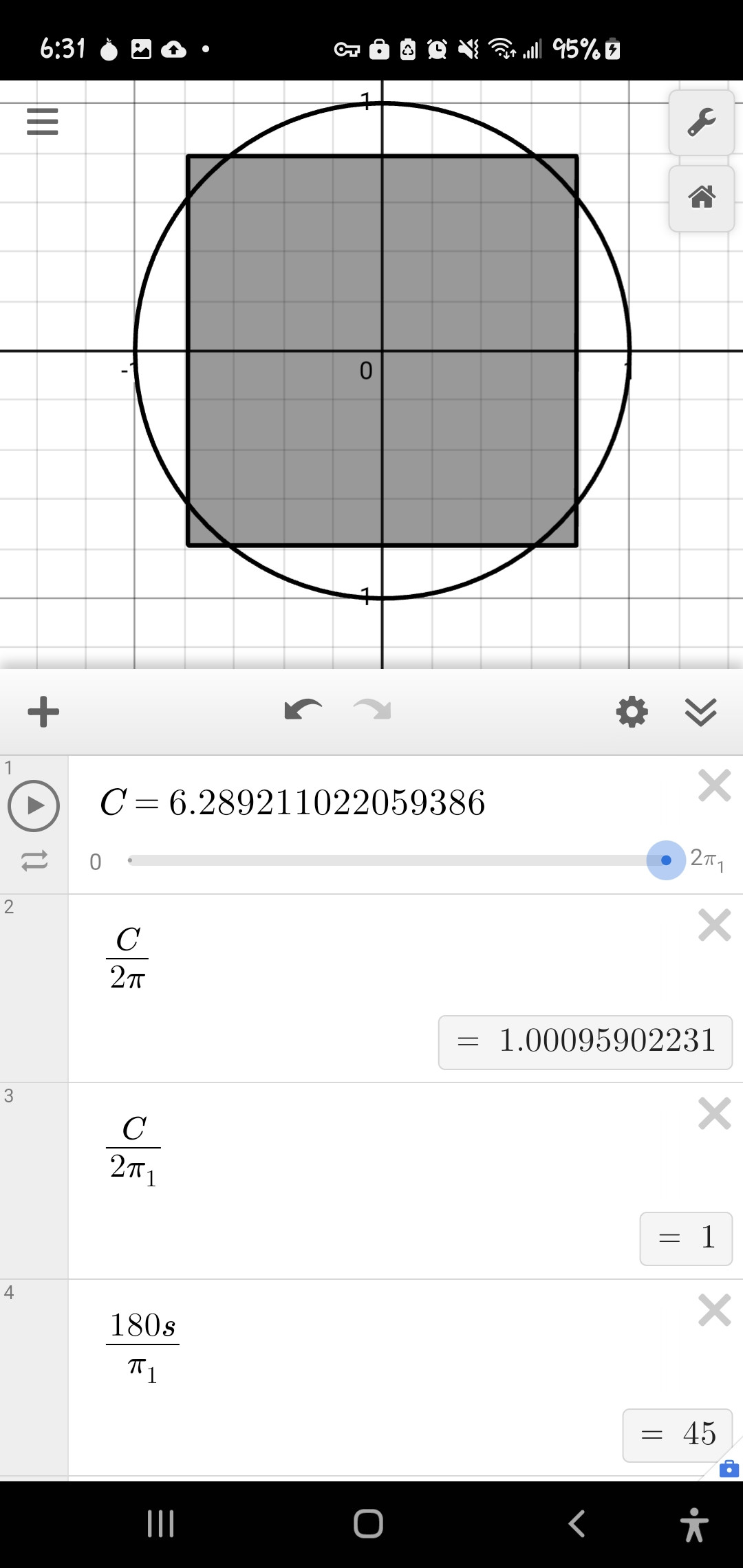
A circle and a square can have the same surface area if the width of the square is located upon the shorter edge of a √φ rectangle, while the diameter of the circle is the same measure as the mean proportional of the √φ rectangle, 𝝿 = 4/√φ:
What you're solving for:
Find the value of 𝜋, such that a circle and a square with specific dimensions have the same area.
What's given in the problem
• The width of the square is the shorter side of a √φ rectangle.
• The diameter of the circle is the mean proportional of the √φ rectangle.
• The Golden ratio of cosine (36 degrees) multiplied by 2 = (φ) = (√(5) plus 1)/2 = 1.618033988749895.
(Phi = (2/((√(5) subtract 1))) = The Golden ratio = 1.618033988749895).
Helpful information:
• The Golden ratio of cosine (36 degrees) multiplied by 2 = (φ) = (√(5) plus 1)/2 = 1.618033988749895.
(Phi = (2/((√(5) subtract 1))) = The Golden ratio = 1.618033988749895).
The mean proportional of a rectangle with sides a and b is √ab.
The area of a square with side s is s squared.
The area of the circle with diameter d 𝝿(d/(2)) squared = 𝝿d squared/(4).
How to solve:
Equate the area of the square and the circle, and solve for 𝝿
Step 1. Define the dimensions of the √φ rectangle
Let the shorter side be 1.
The longer side is then √φ.
Step 2.
The side of the square is 1
.
o The area of the square is 1squared = 1.
.
Step 3.
o The diameter is the mean proportional of the rectangle, √√φ.
Step 4.
o The area of the circle is √√φ times √√φ/√φ = 1.
Step 5. The area of the circle is the same as the area of the square = 1.
The ratio of a circle’s area divided by the radius of the circle times the radius of the circle also equals 𝝿 = 4/√φ, in addition to the ratio of a circle’s circumference divided by a circle’s diameter.
Solve for 𝝿 = 4/√φ:
Area of circle = 1
Area of square = 1.
Width of square = 1.
Diameter of circle = √√φ.
Radius of circle = 0.5 times √√φ.
(1/(0.5 times √√φ times 0.5 times √√φ)) = 𝝿 = 4/√φ = 3.144605511029693144
https://www.google.com/search?q=A+circle+and+a+square+can+have+the+same+surface+area+if+the+width+of+the+square+is+located+upon+the+shorter+edge+of+a+%E2%88%9A%CF%86+rectangle%2C+while+the+diameter+of+the+circle+is+the+same+measure+as+the+mean+proportional+of+the+%E2%88%9A%CF%86+rectangle%2C+%F0%9D%9D%BF+%3D+4%2F%E2%88%9A%CF%86&client=firefox-b-d&sca_esv=cc5939a42d82a808&sxsrf=AHTn8zrt1_JpJiG3I2mrrIonnKiLq1HeLA%3A1744852801139&ei=QVcAaLucCOqthbIPq4-2mAs&ved=0ahUKEwj7wJab892MAxXqVkEAHauHDbMQ4dUDCBA&oq=A+circle+and+a+square+can+have+the+same+surface+area+if+the+width+of+the+square+is+located+upon+the+shorter+edge+of+a+%E2%88%9A%CF%86+rectangle%2C+while+the+diameter+of+the+circle+is+the+same+measure+as+the+mean+proportional+of+the+%E2%88%9A%CF%86+rectangle%2C+%F0%9D%9D%BF+%3D+4%2F%E2%88%9A%CF%86&gs_lp=Egxnd3Mtd2l6LXNlcnAi-wFBIGNpcmNsZSBhbmQgYSBzcXVhcmUgY2FuIGhhdmUgdGhlIHNhbWUgc3VyZmFjZSBhcmVhIGlmIHRoZSB3aWR0aCBvZiB0aGUgc3F1YXJlIGlzIGxvY2F0ZWQgdXBvbiB0aGUgc2hvcnRlciBlZGdlIG9mIGEg4oiaz4YgcmVjdGFuZ2xlLCB3aGlsZSB0aGUgZGlhbWV0ZXIgb2YgdGhlIGNpcmNsZSBpcyB0aGUgc2FtZSBtZWFzdXJlIGFzIHRoZSBtZWFuIHByb3BvcnRpb25hbCBvZiB0aGUg4oiaz4YgcmVjdGFuZ2xlLCDwnZ2_ID0gNC_iiJrPhkgAUABYAHAAeAGQAQCYAQCgAQCqAQC4AQzIAQD4AQGYAgCgAgCYAwCSBwCgBwCyBwC4BwA&sclient=gws-wiz-serp
https://www.google.com/search?q=A+circle+and+a+square+can+have+the+same+surface+area+if+the+width+of+the+square+is+located+upon+the+shorter+edge+of+a+%E2%88%9A%CF%86+rectangle%2C+while+the+diameter+of+the+circle+is+the+same+measure+as+the+mean+proportional+of+the+%E2%88%9A%CF%86+rectangle%2C+%F0%9D%9D%BF+%3D+4%2F%E2%88%9A%CF%86&client=firefox-b-d&sca_esv=cc5939a42d82a808&sxsrf=AHTn8zrt1_JpJiG3I2mrrIonnKiLq1HeLA%3A1744852801139&ei=QVcAaLucCOqthbIPq4-2mAs&ved=0ahUKEwj7wJab892MAxXqVkEAHauHDbMQ4dUDCBA&oq=A+circle+and+a+square+can+have+the+same+surface+area+if+the+width+of+the+square+is+located+upon+the+shorter+edge+of+a+%E2%88%9A%CF%86+rectangle%2C+while+the+diameter+of+the+circle+is+the+same+measure+as+the+mean+proportional+of+the+%E2%88%9A%CF%86+rectangle%2C+%F0%9D%9D%BF+%3D+4%2F%E2%88%9A%CF%86&gs_lp=Egxnd3Mtd2l6LXNlcnAi-wFBIGNpcmNsZSBhbmQgYSBzcXVhcmUgY2FuIGhhdmUgdGhlIHNhbWUgc3VyZmFjZSBhcmVhIGlmIHRoZSB3aWR0aCBvZiB0aGUgc3F1YXJlIGlzIGxvY2F0ZWQgdXBvbiB0aGUgc2hvcnRlciBlZGdlIG9mIGEg4oiaz4YgcmVjdGFuZ2xlLCB3aGlsZSB0aGUgZGlhbWV0ZXIgb2YgdGhlIGNpcmNsZSBpcyB0aGUgc2FtZSBtZWFzdXJlIGFzIHRoZSBtZWFuIHByb3BvcnRpb25hbCBvZiB0aGUg4oiaz4YgcmVjdGFuZ2xlLCDwnZ2_ID0gNC_iiJrPhkgAUABYAHAAeAGQAQCYAQCgAQCqAQC4AQzIAQD4AQGYAgCgAgCYAwCSBwCgBwCyBwC4BwA&sclient=gws-wiz-serp
A circle and a square can have the same surface area if half of the vertical width of the square is located upon the shorter edge of a √φ rectangle, while the radius of the circle is the same measure as the mean proportional of the √φ rectangle, both the radius of the circle and the center of the square are located in the same place, The width of the square is 2 and the radius of the circle is √√φ, 𝝿 = 4/√φ:
What you are solving for,
Confirmation that the area of the circle and the square are the same.
• The Golden ratio of cosine (36 degrees) multiplied by 2 = (φ) = (√(5) plus 1)/2 = 1.618033988749895.
(Phi = (2/((√(5) subtract 1))) = The Golden ratio = 1.618033988749895).
Helpful information:
• The Golden ratio of cosine (36 degrees) multiplied by 2 = (φ) = (√(5) plus 1)/2 = 1.618033988749895.
(Phi = (2/((√(5) subtract 1))) = The Golden ratio = 1.618033988749895).
• The width of the square is 2.
• The radius of the circle is √√φ.
• 𝝿 = 4/√φ.
2 times 2 = 4. The area of a square with a width of 2 = 4.
4/√φ times √√φ times √√φ = 4. The area of a circle with a radius of √√φ = 4, according to 𝝿 = 4/√φ.
The circle and the square have the same surface area that is 4.
The correct value of 𝝿 = Pi = 4/√φ = 3.144605511029693144.
https://measuringpisquaringphi.com/
https://www.google.com/search?client=firefox-b-d&q=A+circle+and+a+square+can+have+the+same+surface+area+if+half+of+the+vertical+width+of+the+square+is+located+upon+the+shorter+edge+of+a+%E2%88%9A%CF%86+rectangle%2C+while+the+radius+of+the+circle+is+the+same+measure+as+the+mean+proportional+of+the+%E2%88%9A%CF%86+rectangle%2C+both+the+radius+of+the+circle+and+the+center+of+the+square+are+located+in+the+same+place%2C+The+width+of+the+square+is+2+and+the+radius+of+the+circle+is+%E2%88%9A%E2%88%9A%CF%86%2C+%F0%9D%9D%BF+%3D+4%2F%E2%88%9A%CF%86
Constructing a straight line equal to pi by using just a compass and a straight edge part1:
The correct value for 𝝿 = pi = 4/√φ = 3.144605511029693144 is NOT transcendental because of the following minimal polynomial that is associated with it:
x4 + 16 x2 – 256
The shortest edge length of a Kepler right triangle is the same measure as the circumference of a circle with a diameter that is equal in measure to 1 quarter of the second longest edge length of the Kepler right triangle, also the second longest edge length of a Kepler right triangle is the same measure as the circumference of a circle with a diameter that is equal in measure to 1 quarter of the hypotenuse of the Kepler right triangle.
If the shortest edge length of an Kepler right triangle is reduced to 1 then the hypotenuse of the Kepler right triangle is equal to the Golden ratio of cosine (36 degrees) multiplied by 2 = (φ) = (√(5) plus 1)/2 = 1.618033988749895, while the second longest edge length of the Kepler right triangle is equal to the Square root of the Golden ratio = √φ = 1.272019649514068, according to the Pythagorean theorem.
Remember that the correct value of 𝝿 = Pi = 4/√φ = 3.144605511029693144.
A straight line exists between 2 points, that are connected together by a straight edge.
If a straight line is constructed and from either end of the straight line 1 quarter of the length of the straight line is used as the shortest edge length of a Kepler right triangle, while the second longest edge length of the Kepler right triangle is used as the diameter of a circle, then the circle with a diameter that is the same measure as the second longest edge length of the Kepler right triangle will have a circumference that is the same measure as the straight line.
Remember that the correct value of 𝝿 = Pi = 4/√φ = 3.144605511029693144.
For example the length of the straight line is 4 equal units of measure and 4/√φ times √φ = 4.
If the second longest edge length of a Kepler right triangle is equal to 4 times the diameter of a circle then the shortest edge length of a Kepler right triangle is the same measure as the circumference of a circle with a diameter that is equal to 1 quarter of the second longest edge length of a Kepler right triangle. The ratio of 4 times the diameter of a circle divided by the circumference of a circle = the square root of the Golden ratio phi = √φ = 1.272019649514069.
If the measure for the diameter of a circle is already known especially when the diameter of the circle is a rational measure and the desire is to create a straight line equal to the correct value of 𝝿 = Pi = 4/√φ = 3.144605511029693144 a solution is to multiply the diameter of the circle 4 equal times on a straight line and use 4 times the diameter of the circle on a straight line as the longer measure of a line that is divided into the Golden ratio of cosine (36 degrees) multiplied by 2 = (φ) = (√(5) plus 1)/2 = 1.618033988749895.
The shorter measure of the line that is divided into the Golden ratio of cosine (36 degrees) multiplied by 2 = (φ) = (√(5) plus 1)/2 = 1.618033988749895 is the shortest edge length of a Kepler right triangle, while 4 times the diameter of the circle on a straight line is also the hypotenuse of a Kepler right triangle. The second longest edge length of the smaller mentioned Kepler right triangle is the same measure as the circumference of the circle with a diameter that is equal to 4 times the diameter of the circle on a straight line that is also used as the longer measure of a line that is divided into the Golden ratio of cosine (36 degrees) multiplied by 2 = (φ) = (√(5) plus 1)/2 = 1.618033988749895 and also the hypotenuse of a Kepler right triangle.
The Pythagorean theorem can also be used to confirm the accuracy of the construction for example:
The diameter of the circle is 88.
88 times 4 = 352.
352/(φ) = 217.547964039962966.
352 times 352 = 123904.
352/(φ) times 352/(φ) = 47327.116657933028728.
123904 subtract 352/(φ) times 352/(φ) = 76576.883342066971272.
The square root of 76576.883342066971272 = 276.725284970612997.
(√(123904 subtract 352/(φ) times 352/(φ)) = 276.725284970612997.
(352/√φ) = 276.725284970612997.
((352/√φ)/88) = 𝝿 = Pi = 4/√φ = 3.144605511029693144..
4/√φ times 88 = (352/√φ) = 276.725284970612997.
A circle with a diameter of 88 has a circumference of (352/√φ) = 276.725284970612997 according to the correct value of 𝝿 = Pi = 4/√φ = 3.144605511029693144…
Squaring the circle for equal perimeters – Regarding a circle with a circumference that is the same measure as a square:
Divide the diameter of the circle by the square root of the Golden ratio = √φ = 1.272019649514068 to get 1 quarter of the circle’s circumference, so that a square with a perimeter that is equal in measure to the circumference of a circle can be created.
Divide the radius of the circle by the square root of the Golden ratio = √φ = 1.272019649514068 to get 1 eighth of the circle's circumference, so that a square with a perimeter that is equal in measure to the circumference of a circle can be created.
Multiply the width if a square by the square root of the Goden ratio = √φ = 1.272019649514068 to get the diameter of a circle with a circumference equal in measure to the perimeter of a square.
Multiply the half width if a square by the square root of the Goden ratio = √φ = 1.272019649514068 to get the radius of a circle with a circumference equal in measure to the perimeter of a square.
(If the diameter of a circle is rational while the circumference of the circle is irrational with an infinite decimal expansion then the circumference of the circle can be gained if the diameter of the circle is multiplied by 4 and divided by the square root of the Golden ratio = √φ = 1.272019649514069.
If the circumference of the circle is a rational number while the diameter of the circle is irrational with an infinite decimal expansion then the diameter of the circle can be gained if 1 quarter of the circle’s circumference is multiplied by the square root of the Golden ratio = √φ = 1.272019649514069.
If the circumference of the circle is a rational number while the diameter of the circle is irrational with an infinite decimal expansion then the diameter of the circle can also be gained if the circumference of the circle is multiplied by the square root of the Golden ratio = √φ = 1.272019649514069 and the result of multiplying the circumference of the circle by the square root of the Golden ratio = √φ = 1.272019649514069 is divided by 4.
If both the circumference of the circle and the diameter of the circle are irrational with an infinite decimal expansion then the circumference of the circle or the diameter of the circle can be gained if either the circumference of the circle or the diameter of the circle is divided by the square root of 5 = 2.23606797749979, or if that does NOT work then the circumference of the circle or the diameter of the circle can be divided by the Golden ratio of cosine (36 degrees) multiplied by 2 = (φ) = (√(5) plus 1)/2 = 1.618033988749895, or if that does NOT work then the circumference of the circle or the diameter of the circle can be divided by the square root of the Golden ratio = √φ = 1.272019649514069, or if that does NOT work then the circumference of the circle or the diameter of the circle can be divided by the square root of the square root of the Golden ratio = √√φ = 1.127838485561682 , or if that does NOT work then the circumference of the circle or the diameter of the circle can be divided by 𝝿 = Pi = 4/√φ = 3.144605511029693144.
The irrational decimal expansion of the circumference of a circle and the diameter of a circle can be multiples of:
the square root of 5 = 2.23606797749979, or multiples of the Golden ratio of cosine (36 degrees) multiplied by 2 = (φ) = (√(5) plus 1)/2 = 1.618033988749895, or multiples of the square root of the Golden ratio = √φ = 1.272019649514069, or multiples of the square root of the square root of the Golden ratio = √√φ = 1.127838485561682 or multiples of 𝝿 = Pi = 4/√φ = 3.144605511029693144.
If the measure of the circle’s diameter is already known and identified while the measure of the circle’s circumference is unknown and NOT identified then the circumference of the circle can be gained if 𝝿 = Pi = 4/√φ = 3.144605511029693144 is multiplied by the measure of the circle’s diameter.
If the measure of a circle’s circumference is already known and identified while the measure of the circle’s diameter is unknown and NOT identified then the diameter of the circle can be gained if the circle’s circumference is divided by 𝝿 = Pi = 4/√φ = 3.144605511029693144).
Pythagorean theorem:
https://en.wikipedia.org/wiki/Pythagorean_theorem
The correct value of 𝝿 = Pi = 4/√φ = 3.144605511029693144
www.measuringpisquaringphi.com
https://www.wolframalpha.com/input?i=4%2F%E2%88%9A%CF%86+%3D
Constructing a straight line equal to pi by using just a compass and a straight edge part 2:
A line equal to 𝝿 = Pi = 4/√φ = 3.144605511029693144 can also be constructed with only compass and straight edge and also a stylus from a square and a circle with the same surface area because if the edge of a square is multiplied by √√φ = 1.127838485561682 then the result is the diameter of a circle with the same surface area as the square and if the perimeter of a square is divided by √√φ = 1.127838485561682 the result is the circumference of a circle with the same surface area as the square.
Circumference of circle divided by diameter of circle = 𝝿 = pi = 4/√φ = 3.144605511029693144.
A Kepler right triangle is half of a square root of the Golden ratio = √φ = 1.272019649514068 rectangle. The hypotenuse of a Kepler right triangle can also be the diagonal of a square root of the Golden ratio = √φ = 1.272019649514068 rectangle.
If the longer measure of a square root of the Golden ratio = √φ = 1.272019649514068 rectangle is the same measure as the perimeter of a square then the mean proportional of that square root of the Golden ratio = √φ = 1.272019649514068 rectangle, that is also the square root of the surface area of that square root of the Golden ratio = √φ = 1.272019649514068 rectangle is the same measure as the circumference of a circle with the same surface area as the square with a perimeter that is equal in measure to the longer measure of the square root of the Golden ratio = √φ = 1.272019649514068 rectangle.
The surface area of a rectangle can be derived if the shorter measure of the rectangle is multiplied by the measure of the longer edge of the rectangle.
If the measure for the width of a square is already known especially when the width of the square is a rational measure and the desire is to create a straight line equal to the correct value of 𝝿 = Pi = 4/√φ = 3.144605511029693144 a solution is to multiply the width of the square 4 equal times on a straight line and use the perimeter of the square on a straight line as the longer measure of a line that is divided into the Golden ratio of cosine (36 degrees) multiplied by 2 = (φ) = (√(5) plus 1)/2 = 1.618033988749895.
The shorter measure of the line that is divided into the Golden ratio of cosine (36 degrees) multiplied by 2 = (φ) = (√(5) plus 1)/2 = 1.618033988749895 is the shortest edge length of a Kepler right triangle, while the perimeter of the square on a straight line is also the hypotenuse of the smaller Kepler right triangle. The second longest edge length of the smaller mentioned Kepler right triangle is the shortest measure of the largest Kepler right triangle with its second longest edge length equal to the perimeter of the mentioned square on a straight line that is also used as the longer measure of a line that is divided into the Golden ratio of cosine (36 degrees) multiplied by 2 = (φ) = (√(5) plus 1)/2 = 1.618033988749895 and also the hypotenuse of a smaller Kepler right triangle.
The Pythagorean theorem can also be used to confirm the accuracy of the construction for example:
The width of the square is 66 equal units of measure.
66 times 4 = 264.
264/(φ) = 163.16097302997224.
264 times 264 = 69696.
264/(φ) times 264/(φ) = 26621.50312008732866.
69696 subtract 264/(φ) times 264/(φ) = 43074.49687991267134.
The square root of 43074.49687991267134 = 207.543963727959748.
(√(69696 subtract 264/(φ) times 264/(φ)) = 207.543963727959748.
(264/√φ) = 207.543963727959748.
The longer edge of the square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle is 264 equal units of measure.
The shorter edge of the square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle is (264/√φ) = 207.543963727959748.
((264/√φ) times 264) = 54791.606424181373346.
The surface area of a square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle with its longer edge equal to 264 equal units of measure, while its shorter edge is equal to (264/√φ) = 207.543963727959748 is ((264/√φ) times 264) = 54791.606424181373346.
The mean proportional of a square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle with its longer edge equal to 264 equal units of measure while its shorter edge is equal to (264/√φ) = 207.543963727959748 is √((264/√φ) times 264) = 234.076069738410836.
((264/√φ) times √√φ) = 234.076069738410836.
If the measure of the longer edge length of the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle = 264 and the shorter measure of the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle are both combined as the measure for the diameter of a semicircle then the mean proportional of the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle can be located between the corner that has the shorter measure of the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle and the circumference of a semicircle with a diameter that is made from the combined measures of the longer edge length of the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle = 264 and the shorter measure of the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle = (264/√φ) = 207.543963727959748 that are combined to be used as the diameter of a semicircle.
The width of the square is 66 equal units of measure and is also 1 quarter of the longer edge length of the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle = 264.
The edge of the square that is located on the mean proportional of the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle also emanates from the origin point of the mean proportional of the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle, that is the corner or the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle that is connected to the shorter edge of the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle.
If the edge of the square that is located on the mean proportional of the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle that also emanates from the origin point of the mean proportional of the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle, that is the corner or the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle that is connected to the shorter edge of the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle is used as the shorter measure of another square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle then the mean proportional of this new square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle is the diameter of a circle with a circumference that is equal to the mean proportional of the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle.
The circle with a circumference that is equal to the mean proportional of the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle also has the same surface area as the square with a width of 66 equal units of measure.
For example:
The width of the square = 66 equal units of measure.
66 times 264.
The longer edge length of the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle = 264 equal units of measure.
The shorter edge length of the of the largest square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle = (264/√φ) = 207.543963727959748.
The mean proportional of a square root of the Golden ratio phi = √φ = 1.272019649514069 rectangle with its longer edge equal to 264 equal units of measure while its shorter edge is equal to (264/√φ) = 207.543963727959748 is √((264/√φ) times 264) = 234.076069738410836.
√((264/√φ) times 264) = 234.076069738410836.
((264/√φ) times √√φ) = 234.076069738410836.
66 times √√φ = 74.437340047071029.
(((264/√φ) times √√φ)/(66 times √√φ) = 𝝿 = Pi = 4/√φ = 3.144605511029693144..
4/√φ times 66 times √√φ = ((264/√φ) times √√φ) = 234.076069738410836.
A circle with a diameter of 66 times √√φ = 74.437340047071029 has a circumference of ((264/√φ) times √√φ) = 234.076069738410836 according to the correct value of 𝝿 = Pi = 4/√φ = 3.144605511029693144…
The width of the square = 66 equal units of measure.
66 times 66 = 4356.
The diameter of the circle = 66 times √√φ = 74.437340047071029.
4/√φ times 33 times √√φ times 33 times √√φ = 4356.
The equations above demonstrate that a square with a width of 66 equal units of measure has the same surface area as a circle with a diameter of 66 times √√φ = 74.437340047071029 according to the correct value of 𝝿 = Pi = 4/√φ = 3.144605511029693144…
Squaring the circle for the creation of a circle and a square with equal areas:
Divide the diameter of the circle by the square root of the square root of the Golden ratio = √√φ = 1.127838485561682 to get the width of a square with the same surface area of the mentioned circle.
Divide the radius of the circle by the square root of the square root of the Golden ratio = √√φ = 1.127838485561682 to get half the width of a square with the same surface area of the mentioned circle.
Multiply the width of the square by the square root of the square root of the Golden ratio = √√φ = 1.127838485561682 to get the diameter of the circle with the same surface area as the mentioned square.
Multiply half the width of the square by the square root of the square root of the Golden ratio = √√φ = 1.127838485561682 to get half the radius of the circle with the same surface area as the mentioned square.
Divide the perimeter of the square by the square root of the square root of the Golden ratio = √√φ = 1.127838485561682 to get the circumference of a circle with the same surface area as the mentioned square.
If the diameter of a circle is a rational measure then a square with a perimeter that is 4 times the diameter of the circle can be used to determine the surface area of the circle if the surface area of the square is divided by the square root of the Golden ratio = √φ = 1.272019649514069.( If the diameter of a circle is a rational measure then the surface area of the circle can also be known if the diameter of the circle is multiplied by the diameter of the circle and the result of the diameter of the circle that is multiplied by the diameter of the circle is divided by the square root of the Golden ratio = √φ = 1.272019649514069).
“If the diameter of a sphere is a rational measure then a square with a perimeter that is 4 times the diameter of the sphere can be used to determine the surface area of the circle that has a diameter that is the same measure as the diameter of the sphere.
The surface area of a sphere is 4 times the surface area of a circle with a diameter that is the same measure as the sphere.
If the surface area of the square that has a width that is the same measure as the sphere is discovered and multiplied by 4 and is divided by the square root of the Golden ratio = √φ = 1.272019649514069 the result is the surface area of the sphere”.
(If the diameter of a sphere is a rational measure then the surface area of the sphere can also be known if the diameter of the sphere is multiplied by the diameter of the sphere and the result of the diameter of the sphere that is multiplied by the diameter of the sphere is multiplied by 4 and divided by the square root of the Golden ratio = √φ = 1.272019649514069).
Pythagorean theorem:
https://en.wikipedia.org/wiki/Pythagorean_theorem
The correct value of 𝝿 = Pi = 4/√φ = 3.144605511029693144
www.measuringpisquaringphi.com
https://www.wolframalpha.com/input?i=4%2F%E2%88%9A%CF%86+%3D
Quadrature rectangle squared circle with equal areas.
The correct value of 𝝿 = Golden 𝝿 = Pi = 4/√φ = 3.144605511029693144.
45 times √φ = 57.240884228133103 degrees = 1 radian.
(180/(4/√φ)) = 57.240884228133103 degrees = 1 radian.
Phi = (2/((√(5) subtract 1))) = The Golden ratio = 1.618033988749895.
The square root of the Golden ratio = √φ = 1.272019649514069.
(√φ-1) = 0.272019649514069.
(√(√(φ)-1) = 0.521555030187677.
1/(√(√(φ)-1) = 1.917343218107125.
(ATAN(√(√(φ)-1)) degrees =
(ATAN(√(√(φ)-1)) = 27.544519746533803 degrees = 0.481203603297869 radians.
ATAN(1/(√(√(φ)-1))) degrees =
ATAN(1/(√(√(φ)-1))) = 62.455480253466185 degrees = 1.091099152216977 radians.
Another method that can be used to derive the radius of a circle that has the same surface area as a square when the square has to be created before the circle.
Divide half the edge of the square into 4 equal parts and then create a √φ = 1.272019649514069 rectangle with its shortest edge length being equal to 1 quarter of half the edge of the square. Remember that half of a √φ = 1.272019649514069 rectangle is a Kepler right triangle. Multiply the mean proportional of the √φ = 1.272019649514069 rectangle 4 equal times to derive the radius of a circle that has the same surface area as the square that has had half of its edge length divided into 4 equal parts. The radius of a circle is half the diameter of a circle.
A mean proportional is the square root for the surface area of a rectangle.
The surface area of a rectangle can be derived by multiplying the shorter edge length of the rectangle times the length of the longer edge of the rectangle.
If the shorter edge length of a rectangle is 1 while the longer edge length of the rectangle is equal to the √φ = 1.272019649514069 then the surface area of the rectangle will also be the √φ = 1.272019649514069, while the mean proportional of 1 to √φ = 1.272019649514069 rectangle is equal to the √√φ = The square root of the square root of Phi = 1.127838485561682.
If the shorter edge length of a rectangle is 4 while the longer edge length of the rectangle is equal to 4 times the √φ = 1.272019649514069 = the ratio 5.088078598056276 then the surface area of the rectangle will also be equal to 4 times the √φ = 1.272019649514069 = the ratio 5.088078598056276, while the mean proportional of the 4 to 4 times √φ = 1.272019649514069 = rectangle the ratio 5.088078598056276 is equal to 4 times the √√φ = The square root of the square root of Phi = 1.127838485561682 = the ratio 4.511353942246728.
The longer edge of a Phi = (√(5) +1)/2 = The Golden ratio = 1.618033988749895 rectangle is same measure as the diagonal of a √φ = 1.272019649514069 rectangle with its shortest edge length being equal to the Phi = (√(5) +1)/2 = The Golden ratio = 1.618033988749895 rectangle.
Please remember that the ratio √√φ = 1.127838485561682 is the square root of the ratio √φ = 1.272019649514069 and the ratio 1.272019649514069 is the square root of the Golden ratio of cosine (36 degrees) multiplied by 2 = 1.618033988749895
𝝿 = Pi = 4/√φ = 3.144605511029693144.
Another method that can be used to derive the width of a square that has the same surface area as a circle when the circle has to be created before the square.
If 1 quarter of the radius of a circle is equal in measure to the longer length of a √φ = 1.272019649514069 rectangle then the mean proportional of √φ = 1.272019649514069 rectangle that has its longer edge equal to 1 quarter of the radius of a circle is equal to 1 eighth of the width of a square that has the same surface area as the circle.
A mean proportional is the square root for the surface area of a rectangle.
The surface area of a rectangle can be derived by multiplying the shorter edge length of the rectangle times the length of the longer edge of the rectangle.
If the shorter edge length of a rectangle is 1 while the longer edge length of the rectangle is equal to the √φ = 1.272019649514069 then the surface area of the rectangle will also be the √φ = 1.272019649514069, while the mean proportional of 1 to √φ = 1.272019649514069 rectangle is equal to the √√φ = The square root of the square root of Phi = 1.127838485561682.
If the shorter edge length of a rectangle is 4 while the longer edge length of the rectangle is equal to 4 times the √φ = 1.272019649514069 = the ratio 5.088078598056276 then the surface area of the rectangle will also be equal to 4 times the √φ = 1.272019649514069 = the ratio 5.088078598056276, while the mean proportional of the 4 to 4 times √φ = 1.272019649514069 = rectangle the ratio 5.088078598056276 is equal to 4 times the √√φ = The square root of the square root of Phi = 1.127838485561682 = the ratio 4.511353942246728.
The longer edge of a Phi = (√(5) +1)/2 = The Golden ratio = 1.618033988749895 rectangle is same measure as the diagonal of a √φ = 1.272019649514069 rectangle with its shortest edge length being equal to the Phi = (√(5) +1)/2 = The Golden ratio = 1.618033988749895 rectangle.
Please remember that the ratio √√φ = 1.127838485561682 is the square root of the ratio √φ = 1.272019649514069 and the ratio 1.272019649514069 is the square root of the Golden ratio of cosine (36 degrees) multiplied by 2 = 1.618033988749895
𝝿 = Pi = 4/√φ = 3.144605511029693144.
Creating a square and a circle with the same surface are with the square being created first. Circle and square share the same center in this example.
- Create a square and divide the square into 4 equal parts.
Use half the central height of the square as the longer length of a vertical line that has been divided into Phi = (√(5) +1)/2 = The Golden ratio = 1.618033988749895.
Use half the vertical height of the square plus the result of dividing half the vertical height of the square into Phi = (√(5) +1)/2 = The Golden ratio = 1.618033988749895 combined together as the diagonal of a √φ = 1.272019649514069 rectangle that has its shorter edge length being equal to half the edge of the square.
The mean proportional of the √φ = 1.272019649514069 rectangle that has its shorter edge length being equal to half the edge of the square is equal in measure to the radius of a circle that has the same surface area as the square.
Use half the central height of the square as the longer length of a √φ = 1.272019649514069 rectangle.
The mean proportional of the √φ = 1.272019649514069 rectangle that has its longer edge length being equal to half the edge of the square is equal in measure to 1 eighth of the circumference of a circle that has the same surface area as the square.
A Kepler right triangle is also 1 half of a √φ = 1.272019649514069 rectangle. If the shortest edge length of a Kepler right triangle is equal in measure to 1 eighth of the circumference of a circle then the second longest edge length of the Kepler right triangle is equal in measure to the radius of a circle that has the same surface area as the mentioned square that has half of its vertical height as the shorter edge length of a √φ = 1.272019649514069 rectangle with a mean proportional that is also equal in measure to the radius of a circle with the same surface area as the square.
.
- If a square is divided into 4 equal parts and then another square that is equal in measure to half the edge of the square is added to the edge of the square resulting in 3 squares of equal size then if half the square is used as the longer length of a line that has been divided into Phi = (√(5) +1)/2 = The Golden ratio = 1.618033988749895 then the half the edge of the largest square plus the result of dividing half the edge of the largest square that is made up of 4 smaller squares into Phi = (√(5) +1)/2 = the Golden ratio = 1.618033988749895 combined is equal to the diagonal of a √φ = 1.272019649514069 rectangle that has its shorter edge length being equal to half the width of the largest square.
The mean proportional of the √φ = 1.272019649514069 rectangle that has its shorter edge length being equal to half the edge of the largest square is equal in measure to the radius of a circle that has the same surface area as the largest square.
The radius of the circle that has the same surface area as the square is the second longest edge length of an illumien right triangle, while half the width of the square is the shortest edge length of an Illumien right triangle.
Half the width of the square that has the same surface area of the concerned circle is equal to the shortest edge length of a Kepler right triangle. Add the shortest edge length of the Kepler right triangle to the second longest edge length of the Kepler right triangle to get a (1 plus √φ) = 2.272019649514069 rectangle.
The mean proportional of the (1 plus √φ) = 2.272019649514069 rectangle can either be the shortest edge length of an Illumien right triangle or the hypotenuse of an illumien right triangle if the shortest edge length of the Illumien right triangle is the same measure as the shortest edge length of the original Kepler right triangle that was first used to create the illumine right triangle with its hypotenuse as the same measure as the mean proportional of the (1 plus √φ) = 2.272019649514069 rectangle that was also used to create the appropriate Illumien right triangle.
Half the width of the square that has the same surface area of the concerned circle is equal to the shortest edge length of a Kepler right triangle. Add the shortest edge length of the Kepler right triangle to the second longest edge length of the Kepler right triangle 2 equal times to get a (2 plus √φ) = 3.272019649514069 rectangle.
The mean proportional of the (2 plus √φ) = 3.272019649514069 rectangle is the diagonal of a Locun ratio √(√φ plus 1) = 1.507322012548768 rectangle.
The ratio of the diagonal of a Locun ratio √(√φ plus 1) = 1.507322012548768 rectangle divided by the shorter edge length of the ratio rectangle is (√(√φ plus 2)) = 1.808872480169365.
If a square and a circle are created with the same surface area and the radius of the circle is used as the height of a Pyramid and half the width of the square base Pyramid is used as the shortest edge length of a Illumien right triangle then the hypotenuse of the Illumien right triangle is the same measure as the slant height of the Pyramid with a height that is the same measure as the radius of a circle with the same surface area as the square base Pyramid.
If a square and a circle are created with the same surface area and the radius of the circle is used as the height of a Pyramid and half the width of the square base Pyramid is used as the shorter edge length of a a Locun ratio √(√φ plus 1) = 1.507322012548768 rectangle then the diagonal of the Locun ratio √(√φ plus 1) = 1.507322012548768 rectangle is the same measure as the edge height of the Pyramid with a height that is the same measure as the radius of a circle with the same surface area as the square base Pyramid.
Remember that if the hypotenuse of a Illumien right triangle is divided by the shortest edge length of a Illumien right triangle the result is the Locun ratio √(√φ plus 1) = 1.507322012548768.
Remember that if the second longest edge length of a Illumien right triangle is divided by the shortest edge length of a Illumien right triangle the result is the Locun ratio √√φ = 1.127838485561682.