C.B. : 𝝿 cannot be transcendental because (4/√(48908982/30169519)) divided by 𝝿 = 1
𝝿 cannot be transcendental because (4/√(48908982/30169519))/𝝿 = 1
𝝿 = (4/√(48908982/30169519)) = 3.141592653589793.
(4/√(48908982/30169519)) = :
https://www.google.com/search?client=firefox-b-d&q=%284%2F%E2%88%9A%2848908982%2F30169519%29%29+%3D+
(4/√(48908982/30169519)) = 3.141592653589793.
Traditional 𝝿 = Pi = 4 divided by the square root of = 1.621138938277405 = 𝝿 = 3.141592653589793 is an algebraic number that most mathematicians claim is Transcendental but the following minimal polynomial has been found for Traditional 𝝿 = Pi = (4/√(48908982/30169519)) = 3.141592653589793.
Minimal polynomial: 24454491 x2 – 241356152
https://www.wolframalpha.com/input/?i=is+4+divided+by+the+square+root+of+1.621138938277405+algebraic+%3F
Traditional 𝝿 = Pi = (4/√(48908982/30169519)) = 3.141592653589793 is false.
The correct value of 𝝿 = Pi = 4/√φ = 3.144605511029693144.
𝝿 = Pi = 4/√φ = 3.144605511029693144.
(15 decimal places). 𝝿 = Pi = 4/√φ = 3.144605511029693.
(18 decimal places). 𝝿 = Pi = 4/√φ = 3.144605511029693144.
(50 decimal places) 𝝿 = Pi = 4/√φ = 3.14460551102969314427823434337183571809248823135089
(60 decimal places) 𝝿 = Pi = 4/√φ = 3.14460551102969314427823434337183571809248823135089295065961
Traditional 𝝿 = Pi = (4/√(48908982/30169519)) = 3.141592653589793 is false.
Minimal polynomial: 24454491 x2 – 241356152
The correct value of 𝝿 = Pi = 4/√φ = 3.144605511029693144.
www.measuringpisquaringphi.com
For comparisons:
𝝿 vs. (4/(√(1/2 plus √(5)/2))) and (4/(𝝿)) vs. (√(1/2 plus √(5)/2)) and (√(4/𝝿)) vs. (√√(1/2 plus √(5)/2)) and (√𝝿) vs. (2/√√(1/2 plus √(5)/2)):
https://www.google.com/search?q=%F0%9D%9D%BF+vs.+%284%2F%28%E2%88%9A%281%2F2+plus+%E2%88%9A%285%29%2F2%29%29%29+and+%284%2F%28%F0%9D%9D%BF%29%29+vs.+%28%E2%88%9A%281%2F2+plus+%E2%88%9A%285%29%2F2%29%29+and+%28%E2%88%9A%284%2F%F0%9D%9D%BF%29%29+vs.+%28%E2%88%9A%E2%88%9A%281%2F2+plus+%E2%88%9A%285%29%2F2%29%29+and+%28%E2%88%9A%F0%9D%9D%BF%29+vs.+%282%2F%E2%88%9A%E2%88%9A%281%2F2+plus+%E2%88%9A%285%29%2F2%29%29&client=firefox-b-d&sca_esv=242238691926b20a&sxsrf=AHTn8zpxtY32sSVLgWpKD9Ec9CxoClYE_g%3A1744242402236&ei=4gb3Z5GYDsTvi-gP58KXiQ0
𝝿 vs. (4/(√φ)) and (4/(𝝿)) vs. (√φ) and (√(4/𝝿)) vs. (√√φ) and (√𝝿) vs. (2/√√φ):
https://www.google.com/search?client=firefox-b-d&q=%F0%9D%9D%BF+vs.+%284%2F%28%E2%88%9A%CF%86%29%29+and+%284%2F%28%F0%9D%9D%BF%29%29+vs.+%28%E2%88%9A%CF%86%29+and+%28%E2%88%9A%284%2F%F0%9D%9D%BF%29%29+vs.+%28%E2%88%9A%E2%88%9A%CF%86%29+and+%28%E2%88%9A%F0%9D%9D%BF%29+vs.+%282%2F%E2%88%9A%E2%88%9A%CF%86%29
Regarding squaring the circle, √𝝿 vs. (2/√√(1/2 plus √(5)/2)):
https://www.google.com/search?client=firefox-b-d&q=%E2%88%9A%F0%9D%9D%BF+vs.+%282%2F%E2%88%9A%E2%88%9A%281%2F2+plus+%E2%88%9A%285%29%2F2%29%29
Regarding squaring the circle, √𝝿 vs. (2/(√√φ)):
https://www.google.com/search?client=firefox-b-d&q=%E2%88%9A%F0%9D%9D%BF+vs.+(2%2F(%E2%88%9A%E2%88%9A%CF%86))
The square root of Phi = √φ = 1.272019649514069. (-1 - x2 + x4)
http://www.wolframalpha.com/input/?i=%E2%88%9A%CF%86
The square root of the square root of Phi = √√φ = 1.127838485561682.
sqrt[sqrt(phi)] √√φ:
http://www.wolframalpha.com/input/?i=√√φ
(-1 - x4 + x8)
(x8 - x4 – 1)
Archimedes value for pi is wrong because it is impossible for a polygon with an infinite amount of edges to exist, a polygon cannot become a circle because a circle does not have any edges:
While Archimedes' method of using polygons to approximate pi is a brilliant and foundational concept, it's important to understand that a circle isn't a polygon with an infinite number of sides, but rather the limit of polygons as the number of sides increases infinitely.
Here's a breakdown:
• Archimedes' Method:
Archimedes used inscribed and circumscribed polygons (polygons inside and outside a circle) to find an approximate value for pi (π), the ratio of a circle's circumference to its diameter.
• Approximation, Not Exact:
He recognized that as the number of sides of the polygons increased, their perimeters got closer and closer to the circumference of the circle, thus refining the approximation of pi.
• Limit, Not Infinity:
Mathematicians today would use the concept of limits to describe this, saying that a circle is the limit of regular polygons with an increasing number of sides, not that a circle is a polygon with an infinite number of sides.
• Pi as an Irrational Number:
Pi is an irrational number, meaning it cannot be expressed as a simple fraction and has an infinite number of non-repeating digits after the decimal point.
• Archimedes's Result:
Archimedes showed that pi is between 3 1/7 and 3 10/71.
• Why it's not a polygon:
A polygon is defined by having straight sides and angles, whereas a circle has a continuous, curved boundary.
• Focus on the Limit:
The key is to understand that the circle is the result of the limiting process of polygons with increasing sides, not a polygon itself.
https://www.google.com/search?q=archimedes-value-for-pi-is-wrong-because-it-is-impossible-for-a-polygon-with-an-infinite-amount-of-edges-to-exist%2C+a-polygon-cannot-become-a-circle-because-a-circle-does-not-have-any-edges&sca_esv=b275642f2649e319&sxsrf=AHTn8zpFU02ov97DSiF-ivgfVgJJTNpJ6A%3A1742599658710&ei=6vXdZ8mPK5OChbIPo4--wQ4
Traditional 𝝿 = Pi = (51066975/16255123) = 3.141592653589793 is false.
Traditional 𝝿 = Pi = (10 ^ 12)/(16255123/10213395)/(2)/(10 ^ 11) = 3.141592653589793 is false and is also the result of the perimeter of a regular polygon with more than a trillion edges divided by the diagonal of the polygon that has a perimeter with more than a trillion edges.
Perimeter of the regular polygon = 1000,000,000,000,000,000,000,000,000,000,000,000,000,000.
That is 1 Plus 42 zeros.
Commas removed = 1000000000000000000000000000000000000000000.
Diagonal of a regular polygon with 1000,000,000,000,000,000,000,000,000,000,000,000,000,000 edges = the ratio 3.183098861837902e + 82.
1000,000,000,000,000,000,000,000,000,000,000,000,000,000
divided by 3.183098861837902e + 82 =
3.14159265358979769496178102.
(10 ^ 42)/(3.183098861837902) = 3.141592653589793.
((10 ^ 42)/(30685681/9640191)) = 3.141592653589793.
Traditional 𝝿 = Pi = with 24 decimal places = 3.141,592,653,5897,976,949,617,8102
Traditional 𝝿 = Pi = with 15 decimal places = 3.141,592,653,589,793.
Regular Polygon calculator. Please remember to use a minimum of 15 digits to be accurate:
http://www.1728.org/polygon.htm
Regarding the chords and arcs of circles:
A chord is a straight line. The edge of a polygon is a straight line.
An arc is a curve. The total arc length of a circle is the full curvature around the circle.
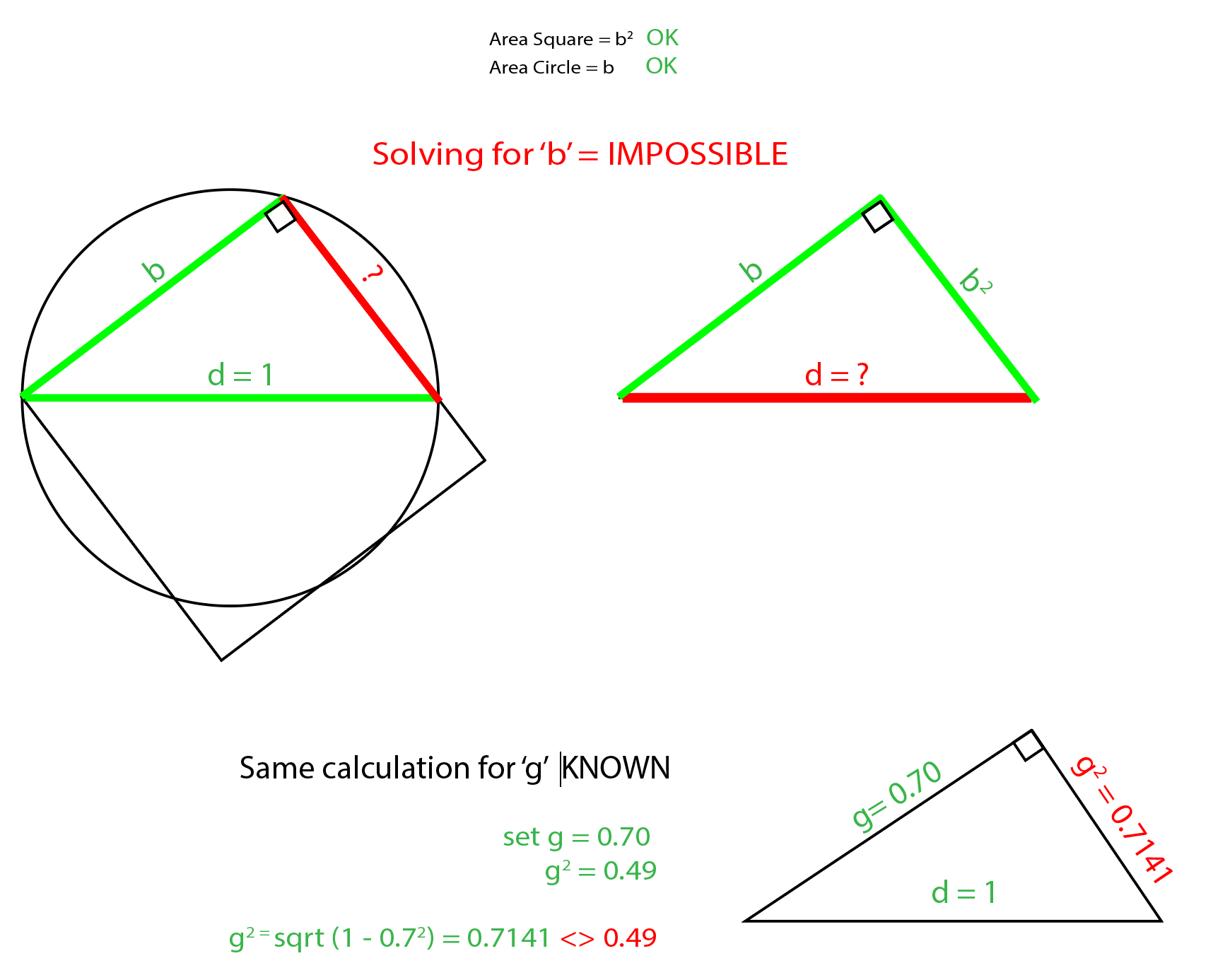
If an arc is attached to a chord in a circle by 2 points on a straight line then the length of the arc is longer than the length of the chord. The correct value of Pi MUST be larger than (4/√(48908982/30169519)), because the arc length of a circle is always longer than the chord length that is connected by 2 points on a straight line inside of a circle.
𝝿 MUST be larger than (4/√(48908982/30169519)) because the circumference of a circle is always longer than the perimeter of any inscribed polygon and as the number of sides of the inscribed polygon increases towards a large number the polygon’s perimeter gets closer to the circumference of the circle, but the perimeter of the polygon will always be shorter than the circumference of the circle.
https://www.google.com/search?client=firefox-b-d&q=A+chord+is+a+straight+line.+The+edge+of+a+polygon+is+a+straight+line.An+arc+is+a+curve.+The+total+arc+length+of+a+circle+is+the+full+curvature+around+the+circle.If+an+arc+is+attached+to+a+chord+in+a+circle+by+2+points+on+a+straight+line+then+the+length+of+the+arc+is+longer+than+the+length+of+the+chord.+The+correct+value+of+Pi+MUST+be+larger+than+%284%2F%E2%88%9A%2848908982%2F30169519%29%29%2C+because+the+arc+length+of+a+circle+is+always+longer+than+the+chord+length+that+is+connected+by+2+points+on+a+straight+line+inside+of+a+circle.%F0%9D%9D%BF+MUST+be+larger+than+%284%2F%E2%88%9A%2848908982%2F30169519%29%29+because+the+circumference+of+a+circle+is+always+longer+than+the+perimeter+of+any+inscribed+polygon+and+as+the+number+of+sides+of+the+inscribed+polygon+increases+towards+a+large+number+the+polygon%E2%80%99s+perimeter+gets+closer+to+the+circumference+of+the+circle%2C+but+the+perimeter+of+the+polygon+will+always+be+shorter+than+the+circumference+of+the+circle.
(Alternate version below):
A chord is a straight line. The edge of a polygon is a straight line.
An arc is a curve. The total arc length of a circle is the full curvature around the circle.
If an arc is attached to a chord in a circle by 2 points on a straight line then the length of the arc is longer than the length of the chord. The correct value of Pi MUST be larger than 3.141592653589793, because the arc length of a circle is always longer than the chord length that is connected by 2 points on a straight line inside of a circle.
𝝿 MUST be larger than 3.141592653589793 because the circumference of a circle is always longer than the perimeter of any inscribed polygon and as the number of sides of the inscribed polygon increases towards a large number the polygon’s perimeter gets closer to the circumference of the circle, but the perimeter of the polygon will always be shorter than the circumference of the circle.
https://www.google.com/search?client=firefox-b-d&q=A+chord+is+a+straight+line.+The+edge+of+a+polygon+is+a+straight+line.An+arc+is+a+curve.+The+total+arc+length+of+a+circle+is+the+full+curvature+around+the+circle.If+an+arc+is+attached+to+a+chord+in+a+circle+by+2+points+on+a+straight+line+then+the+length+of+the+arc+is+longer+than+the+length+of+the+chord.+The+correct+value+of+Pi+MUST+be+larger+than+3.141592653589793%2C+because+the+arc+length+of+a+circle+is+always+longer+than+the+chord+length+that+is+connected+by+2+points+on+a+straight+line+inside+of+a+circle.%F0%9D%9D%BF+MUST+be+larger+than+3.141592653589793+because+the+circumference+of+a+circle+is+always+longer+than+the+perimeter+of+any+inscribed+polygon+and+as+the+number+of+sides+of+the+inscribed+polygon+increases+towards+a+large+number+the+polygon%E2%80%99s+perimeter+gets+closer+to+the+circumference+of+the+circle%2C+but+the+perimeter+of+the+polygon+will+always+be+shorter+than+the+circumference+of+the+circle.
It is known that the curvature of a circle is longer than the chord length for the perimeter of a polygon that is contained inside of the circle and this knowledge makes it evident that the numerical value for the perimeter of a polygon is always the same as the numerical value for the division of the curvature of the circle that contains the polygon.
If the circumference of a circle is divided into 3 equal parts then the circumference of the circle will contain both 3 chords and 3 arcs and the length of 1 of the arcs will be longer than 1 of the 3 chords that make up the circumference of the circle.
If the circumference of a circle is divided into 8 equal parts then the circumference of the circle will contain both 8 chords and 8 arcs and the length of 1 of the arcs will be longer than 1 of the 8 chords that make up the circumference of the circle.
If the circumference of a circle is divided into 12 equal parts then the circumference of the circle will contain both 12 chords and 12 arcs and the length of 1 of the arcs will be longer than 1 of the 12 chords that make up the circumference of the circle.
The curvature of the circle when divided into equal divisions has the same numerical value as the perimeter of a polygon that is contained inside of the circle.
If a polygon is inscribed inside of a circle then the diagonal of the polygon and the diameter of the circle will have the same measure but the total curvature around the circle will be longer in measure than the perimeter of the polygon that is contained inside of the circle.
The correct definition for pi is the ratio for the circumference of a circle divided by the diameter of a circle.
Traditional 𝝿 = Pi = 4 divided by the square root of = 1.621138938277405 = 3.141592653589793 is false and does not come from the ratio for the circumference of a circle divided by the diameter of a circle.
Traditional 𝝿 = Pi = (4/√(48908982/30169519)) = 3.141592653589793 is false.
The correct value for pi cannot be derived from dividing the perimeter of a polygon with a trillion edges by the diagonal of the polygon with a trillion edges.
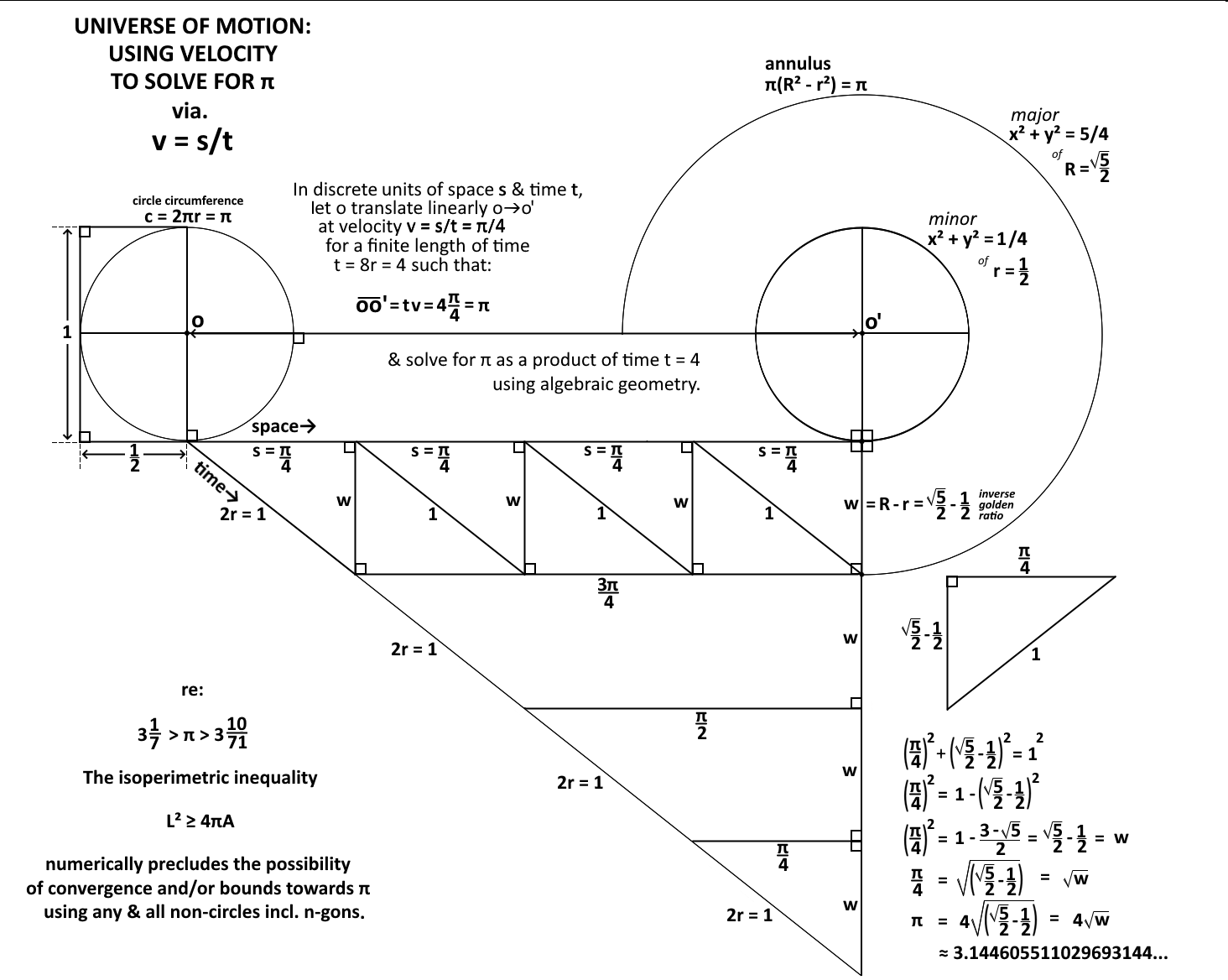
The measure for the curvature of a circle divided by the diameter of the circle produces the correct value for pi = 4 divided by the square root of the golden ratio = 4/√φ = 3.144605511029693144.
To discover the value for the curvature of a circle divided by the diameter of a circle a circle with a 1 meter diameter should be created and the number of times the 1 meter –diameter can be multiplied around the curvature of the circle must be measured and recorded to confirm the correct value of pi.
The measure for the curvature of the circle with a 1-meter diameter must be divided by the 1-meter diameter to confirm the correct value for pi.
Measurements from multiplying a 1-meter diameter for a circle around the curvature of a circle has already been recorded and the correct value for pi have been confirmed to be 3.1446 and not 3.141.
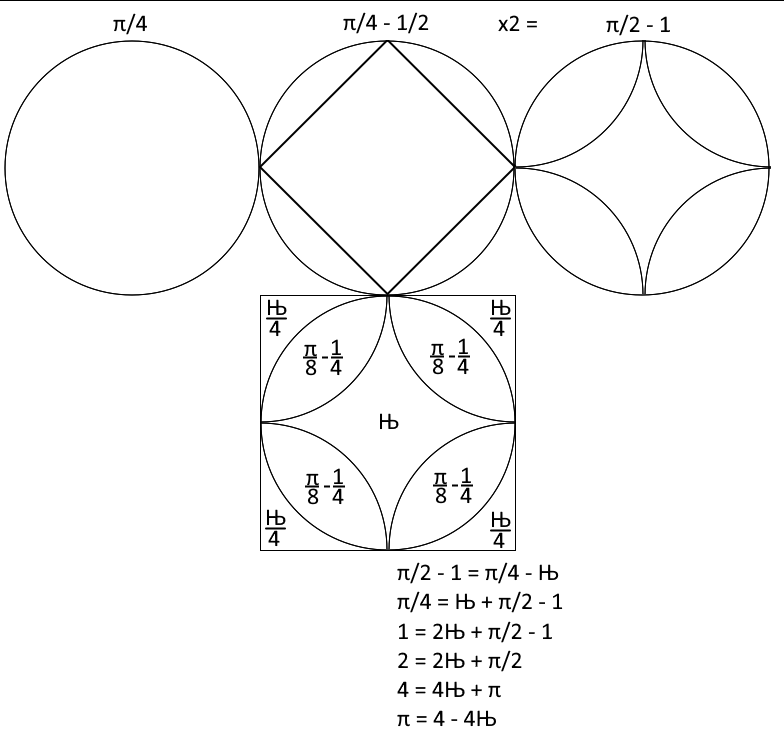
To get the rest of the digits for the true value of pi = 3.1446 a kepler right triangle can be used to create a square that has a perimeter that is equal in measure to the curvature of a circle.
If the second longest edge length for a Kepler right triangle is used as the diameter for a circle then the perimeter of the square that is located upon the shortest edge length for the Kepler right triangle can be confirmed to be the same measure as the curvature of the circle that has a diameter equal in measure to the second longest edge length for the Kepler right triangle.
When the perimeter of the square that is located on the shortest edge length for the Kepler right triangle is divided by the diameter of the circle that is equal in measure to the second longest edge length for the Kepler right triangle the correct value for 𝝿 = Pi = 4/√φ = 3.144605511029693144 is further proven and then the correct value for 𝝿 = Pi = 4/√φ = 3.144605511029693144 is multiplied by the diameter of the circle that is equal in measure to the second longest edge length for the Kepler right triangle the result is that the curvature of the circle is confirmed to be the same measure as perimeter of the square that is located on the shortest edge length for the Kepler.
The arc length of the circle is the same measure as the perimeter of the square because the square root of the golden ratio = √φ = 1.2720196495141 can allow the curvature of a circle to be placed on a straight line by using just compass and straight edge.
The Square root of the Golden ratio can be used to transfer the total curvature of a circle to a straight line. The Square root of the Golden ratio = √φ = 1.2720196495141 can turn curves into straight lines and straight lines back into curves.
The square root of the golden ratio = √φ = 1.2720196495141 can be used to transform curves into straight lines and straight lines into curves.
The claim that the perimeter of the square is the same measure as the arc length of the circle due to the measure of the arc length of the circle being derived with the use of the square root of the golden ratio = √φ = 1.272019649514069 can be confirmed if a circle with a 1-meter diameter is created and the diameter of the circle is multiplied around the curvature of the circle confirming that the correct value for pi must be 3.1446.
The Kepler right triangle also confirms that ratio for a circle’s circumference divided by a circle’s diameter is 3.1446.
THE REAL VALUE OF Pi IS NOT TRANSCENDENTAL BECAUSE THE REAL VALUE OF 𝝿 = PI = 4/√φ = 3.144605511029693144 IS THE ONLY VALUE OF PI THAT CAN FIT THE FOLLOWING POLYNOMIAL EQUATION:
4th dimensional equation/polynomial for Golden 𝝿 = Pi = 4/√φ = 3.144605511029693144:
Minimal polynomial:
x4 + 16x2 – 256 = 0.
Chord (geometry):
https://en.wikipedia.org/wiki/Chord_(geometry)
More dissing of fake Pi:
If you do NOT know what Pi is due to the fact that you have NEVER divided the circumference of a circle by the diameter of a circle with 1-meter diameter then you cannot honestly create boundary limit claims for Pi.
You cannot honestly claim that you know what pi is if you have NEVER measured and counted the amount of times a diameter of 1-meter fits around the curvature of the circle to determine the circumference of the circle for the purpose of dividing the circumference of a circle by the diameter of a circle with a 1-meter diameter.
Because you have NEVER measured and counted the amount of times a diameter of 1-meter fits around the curvature of the circle to determine the circumference of the circle for the purpose of dividing the circumference of a circle by the diameter of a circle with a 1-meter diameter you cannot honestly create a boundary limit for Pi because you do NOT know what pi is yet.
To discover Pi you must divide the measure for the circumference of a circle by the measure for the diameter of a circle or alternatively to discover Pi you must divide the area of a circle by the area of the square that is located on the radius of the circle.
You cannot inscribe circles inside of Polygons and circumscribe circles around Polygons to achieve the circumference of a circle because there is forever a gap between the edges of the polygon that is contained inside of the circle and the curvature of the circle.
The area under the curvature of the circle NEVER disappears regardless of the amount of polygons that are constructed inside of the circle and also around the circle.
It is impossible for a polygon to become a circle because polygons have angles while circles do NOT have any angles.
There is NO such thing as a polygon with an infinite amount of edges. It is impossible for a Polygon with an infinite amount of edges to exist because a Polygon is known and identified by the number of edges that a Polygon has for example a Decagon is known for having 10 edges of equal measure.
Infinity cannot be fully counted.
Anything that can be fully counted is NOT infinite.
The True Value of Pi revealed = 4/√φ = 3.144605511029693144:
https://www.youtube.com/watch?v=AHAOn7UfXt8
The Pi that is equal to 3.141592653589793 that you are using is wrong - ULTIMATE PROOF part 1:
https://www.youtube.com/watch?v=UFh2Imm6Lrk
The Pi that is equal to 3.141592653589793 that you are using is wrong - ULTIMATE PROOF part 2:
https://www.youtube.com/watch?v=PtCyUUBomtM
Proof of Pi = 3.14466 in EQUILATERAL triangle:
https://www.youtube.com/watch?v=AEqzCMKY7lg
Pi: 3.1416 vs. 3.1446:
https://www.youtube.com/watch?v=K1HBn4PV4EE
Algebraic Methods for deriving Traditional P, that is the fake value of 𝝿 = Pi = 3.141592653589793.
Traditional 𝝿 = Pi = (51066975/16255123) = 3.141592653589793 is false (R beware).
Traditional 𝝿 = Pi = (10 ^ 12)/(16255123/10213395)/(2)/(10 ^ 11) = 3.141592653589793 is false.
Traditional 𝝿 = Pi = ((10 ^ 42)/(30685681/9640191)) = 3.141592653589793 is false.
Traditional 𝝿 = Pi = (4/√(48908982/30169519)) = 3.141592653589793 is false.
Traditional 𝝿 = Pi = 4 divided by the square root of = 1.621138938277405 = 𝝿 = 3.141592653589793 is an algebraic number that most mathematicians claim is Transcendental but the following minimal polynomial has been found for Traditional 𝝿 = Pi = (4/√(48908982/30169519)) = 3.141592653589793.
Minimal polynomial: 24454491 x2 – 241356152
https://www.wolframalpha.com/input/?i=is+4+divided+by+the+square+root+of+1.621138938277405+algebraic+%3F
4 divided by the square root of 16/π squared:
https://www.wolframalpha.com/input/?i=4+divided+by+the+square+root+of+16%2F%CF%80+squared
4 divided by 1.273239544735163 = 𝝿 = 3.141592653589793 =
https://www.wolframalpha.com/input/?i=4+divided+by++1.273239544735162686151070106980114896275677165923651589981
sqrt(6 ζ(2)) =
https://www.wolframalpha.com/input/?i=sqrt%286+%CE%B6%282%29%29
16/π squared =
https://www.wolframalpha.com/input/?i=16%2F%CF%80+squared
Possible root plot for 4 divided by the square root of = 1.621138938277405 = 𝝿 = 3.141592653589793:
https://www.wolframalpha.com/input/?i=4+divided+by+the+square+root+of+%3D+1.621138938277405
Fake 𝝿 = Pi = 3.141592653589793 can also be gained through the formula 10 ^ 42/3.183098861837902.
Traditional 𝝿 = Pi = (51066975/16255123) = 3.141592653589793 is false (R beware).
Traditional 𝝿 = Pi = (10 ^ 12)/(16255123/10213395)/(2)/(10 ^ 11) = 3.141592653589793 is false.
https://www.wolframalpha.com/input?i=%2810%5E12%29%2F%2816255123%2F10213395%29%2F%282%29%2F%2810%5E11%29+%3D+
Traditional 𝝿 = Pi = ((10 ^ 42)/(30685681/9640191)) = 3.141592653589793 is false.
https://www.wolframalpha.com/input?i=%28%2810%5E42%29%2F%2830685681%2F9640191%29%29+%3D+
Traditional 𝝿 = Pi = (4/√(48908982/30169519)) = 3.141592653589793 is false.
https://www.wolframalpha.com/input?i=%284%2F%E2%88%9A%2848908982%2F30169519%29%29+%3D+
Many digits of Traditional 𝝿 = Pi = (4/√(48908982/30169519)) =
3.14159265358979251904480570416189286006861842189480475880420990731884333612353733841354162832836010804056689422251380193222791998994021504139522914711744389379529133327714308842825881365854392807323913720167495623618727348936371383480194563961428207745628456026191253072744697921771120118807711604405718783785230468839583603971337186573458585584594057037777493603629178149328526097929262103403898991447622494413648596787236574231735464504722596714513174893573146040795362225970852204886991871955791311912316468502643839111345783341841513610450163748697609517679049116800145540708787970119778094521356961288799413300974053581396455128007263974283232870084580358939506930500288629136682221313299711721234714340855480654601655568659248662918515228637421841252177581791873784774145171169550089155762408731994374241612959817738838504405895548651651863074905268777341310612954441845289018588450378424234517660951581328945943575104408695844331588474222081363974121887108774322532779377468358932351815570496594413212803976091937548952612058596688596381877746927323581925126101382941915918101974293665462847390238203613463656195053357686665218418477189348146688391888145620693869553349682134982039682903004703575966191207775513150863892216000747844272381879567168013706462401039285005832759036178098496282578202298934360376010267382298070916331158378784086280205991585766505332533977609704932010432377251576672432916427564334586727107153496712078553586317657312590770935228449232296242459340075309919774539374093249354931350081045271337811231722255345548795033025989915987773602578746531956812413350663267124687100495947859559238510377734228430187139205866510993894512530156978969549518529805391380958799180890882391036547209954644425487586328713459261595078688973960856911043726326006604957312549383437196884967235557585550547855559806666398552361923191720673638695087793959505616059853789086990483541433941239791198202806672971824196343550724602145889057317511660595567522536263894234960329258275170880607683485337351720514319255118316595726196688362597894991645729482664115027273354032417149124492284068963962522288614391775990444671377410609976257251472349118695033357132860350492706546363441667027509790951687462831220144997335260959269372588890533629824883780112216664294515309172292321339442697773700814342795538873567323431129966056644417330220438260138391608249661293834624892943347442590415541309169525830408457021675554730107388005297443125764409451392680584831978282798318538984344286811601137226719659723194332265692895294087444161736323131876500583729839087804979178379270955539131418160876025800448585882270607851706362969361416735755894685352241680815934250817642289016933779235687458666858794269610936042126104399276004586919974179011348319497668877418254571242200699977786485001174456863152596598182837622167012712709060648600864246303586856203022909989944722904914692936303367634074592894798789111454328974159483910153414915582472673590396669219115741976626932001604102224303371526648859186602860331732713945468126214821357005415493832799263920320776189930988213726371490890270345799586073225678539339161579331586030913419921002485658328161505856962923156588654978768918173348420300504924388003949943883490935304944182064603402850796371102431968094536274856663283308415634665339611870982629824744180621293758411359757767960231800845482898591707339169734657028866723800954479106192445751523666306715993468636023091467523105415326398897734140914969447037396051555800766364819819478415461872101203562836033537123834425348315317765109694781097887015205565343788161457747726331333662632967765193907639483056242711917161896917473151177733350668839317678624373225977430638638429413952393695575606553550070767115099517066047180248261174470297673427193840635196648670567831166549994719928632415776019817518839067349376503736241718598383614994575823118564109643928352294780341767375956704942529042826154734308573002709463042902180286593613053333765026830201785907234333443119343541463253303091535202586093730477353139043527310325688506953196634189818768308763778792560858485862481143945615158960356649315750451737827626069873680256378457115972397895242338228...
Minimal polynomial: 24454491 x2 – 241356152
https://www.wolframalpha.com/input?i=is+%284%2F%E2%88%9A%2848908982%2F30169519%29%29+transcendental%3F+
Many digits of the Golden ratio of cosine (36 degrees) multiplied by 2 = (φ) = (√(5) plus 1)/2 =
1.61803398874989484820458683436563811772030917980576286213544862270526046281890244970720720418939113748475408807538689175212663386222353693179318006076672635443338908659593958290563832266131992829026788067520876689250171169620703222104321626954862629631361443814975870122034080588795445474924618569536486444924104432077134494704956584678850987433944221254487706647809158846074998871240076521705751797883416625624940758906970400028121042762177111777805315317141011704666599146697987317613560067087480710131795236894275219484353056783002287856997829778347845878228911097625003026961561700250464338243776486102838312683303724292675263116533924731671112115881863851331620384005222165791286675294654906811317159934323597349498509040947621322298101726107059611645629909816290555208524790352406020172799747175342777592778625619432082750513121815628551222480939471234145170223735805772786160086883829523045926478780178899219902707769038953219681986151437803149974110692608867429622675756052317277752035361393621076738937645560606059216589466759551900400555908950229530942312482355212212415444006470340565734797663972394949946584578873039623090375033993856210242369025138680414577995698122445747178034173126453220416397232134044449487302315417676893752103068737880344170093954409627955898678723209512426893557309704509595684401755519881921802064052905518934947592600734852282101088194644544222318891319294689622002301443770269923007803085261180754519288770502109684249362713592518760777884665836150238913493333122310533923213624319263728910670503399282265263556209029798642472759772565508615487543574826471814145127000602389016207773224499435308899909501680328112194320481964387675863314798571911397815397807476150772211750826945863932045652098969855567814106968372884058746103378105444390943683583581381131168993855576975484149144534150912954070050194775486163075422641729394680367319805861833918328599130396072014455950449779212076124785645916160837059498786006970189409886400764436170933417270919143365013715766011480381430626238051432117348151005590134561011800790506381421527093085880928757034505078081454588199063361298279814117453392731208092897279222132980642946878242748740174505540677875708323731097591511776297844328474790817651809778726841611763250386121129143683437670235037111633072586988325871033632223810980901211019899176841491751233134015273384383723450093478604979294599158220125810459823092552872124137043614910205471855496118087642657651106054588147560443178479858453973128630162544876114852021706440411166076695059775783257039511087823082710647893902111569103927683845386333321565829659773103436032322545743637204124406408882673758433953679593123221343732099574988946995656473600729599983912881031974263125179714143201231127955189477817269141589117799195648125580018455065632952859859100090862180297756378925999164994642819302229355234667475932695165421402109136301819472270789012208728736170734864999815625547281137347987165695274890081443840532748378137824669174442296349147081570073525457070897726754693438226195468615331209533579238014609273510210119190218360675097308957528957746814229543394385493155339630380729169175846101460995055064803679304147236572039860073550760902317312501613204843583648177048481810991602442523271672190189334596378608787528701739359303013359011237102391712659047026349402830766876743638651327106280323174069317334482343564531850581353108549733350759966778712449058363675413289086240632456395357212524261170278028656043234942837301725574405837278267996031739364013287627701243679831144643694767053127249241047167001382478312865650649343418039004101780533950587724586655755229391582397084177298337282311525692609299594224000056062667867435792397245408481765197343626526894488855272027477874733598353672776140759171205132693448375299164998093602461784426757277679001919190703805220461232482391326104327191684512306023627893545432461769975753689041763650254785138246314658336383376023577899267298863216185839590363998183845827644912459809370430555596137973432613483049494968681089535696348281781288625364608420339465381944194571426668237183949183237090857485026656803989744066210536030640026081711266599541993687316094...
9227465 and 5702887 are both numbers o0f the Fibonacci sequence that culminates in Phi the Golden ratio of 1.6180339887….. .
If 9227465 is divided by 5702887 the result is Phi the Golden ratio = 1.6180339887…
63245986 divided by 39088169 = Phi the Golden ratio = 1.6180339887...
The Golden ratio can also be gained through the formula of the square root of 5 = 2.23606797749979 plus 1 = 3.23606797749979 divided by 2 = 1.6180339887….. .
The Golden ratio can also be gained through the formula in Trigonometry of Cosine (36 degrees) multiplied by 2 = 1.6180339887….. .
The Golden ratio can also be gained through the formula in Trigonometry of Sin (54 degrees) multiplied by 2 = 1.6180339887….. .
The reciprocal of the Golden ratio Phi is 0.6180339887…. and the reciprocal of the Golden ratio Phi can also be gained through the formula in Trigonometry of Cosine (72 degrees) multiplied by 2 = 0.6180339887….. .
Cosine (36 degrees) times 2:
https://www.theproblemsite.com/ask/2016/10/cosine-of-36-degrees
Phi = (1/2 plus √(5)/2) = The Golden ratio = 1.618033988749895.
Phi = (√(5) plus 1)/2 = The Golden ratio = 1.618033988749895.
Phi = (2/((√(5) subtract 1))) = The Golden ratio = 1.618033988749895.
https://www.wolframalpha.com/input/?i=1%2F2+%2B+sqrt%285%29%2F2
Minimal polynomial
x2 - x - 1
https://www.wolframalpha.com/input/?i=x^2+-+x+-+1
The Golden ratio = (φ) = 1.618033988749895 to 1 million decimal places:
https://www.wolframalpha.com/input?i=%28%E2%88%9A%285%29+plus+1%29%2F2+to+1000000+decimal+places
Many digits of the square root of the Golden ratio = (√φ) =
1.27201964951406896425242246173749149171560804184009624861664038253929757553606801183038421498846025853851414763672802650571033811881483526492194484574461860433489454901711190659371547273845503763042645966314657429527810131118752263125934779278490202612992869845106340463643028416191821135398328352285929641919272945192666479908610094800505274468249004066217456802539536429693254790794378637506112352531246919553089942948654095931215799748879524092171982886231477989994626856348173709726662394760795757702837384091820193370999724346715955862112260165678813451637264655901218321162088633129936927599597528207155496460105313816691125491065379052174550143343776455810499628734934067732465962878251506625721897872258517823443781324397350511823752485646711142754624798328310161549347088954999354816753763248108363629773824369644124071938932626473383613521995691897474441052777569924629931351371371575875782426051919061895545328866683834290705951306975615558180842748469317864727132750339635613295551022303724430391033979251737345425941675697696422995462811966016405683559837096487864868577224282233391909777157930692024186461941394068971197405739763134542116462733410052528869538079092774060770641292010540813553272683725965877662226070519371475562649874364619537537779763214330937888867872842680060857527892151854048913101306284019143589502005307616014069518692128139117972935516210944146435960160801578644516728306524933838514732464104550687663464517150869053342698863281632486685921536193496938986048968159954096455660909640476872937723260379420144168109543117693473297130957384462573690111613762636636966173115098805327997412185230411584413071986172327324975454727627296709435491563223316965269050139083093627811927068560142499434921094451557156660490815997862027027912345623726078584039517141912963159090148768218699408879158692276538781019288043320521408128801559146674203607126000009289379000511682529973684147969926849653460649194713537725034742820163102830233202745907863074380688317181980993763719267278043691810658111994996150995932820663273708645799563071070979407002083763833394539116297389137404478414776465830299299692909554858829295004264703031869915650211587462519418007461182669759005762555787161682827523989881240135560561273771920744103084629094144400284891757387531555568690267969884623542980782453127903332165476128620686225029624431043703053923501377577149813476546256492060370590908494211657942658399899299460332717079766677896835655931517311304320590776251005236710928391126512681837423370056877223810348906497329813203112592788616267701569660526080738504439580559875523237526875661315505632294967483691292416597174972326328812569296157799168366350260356673313041023603021304097056513060661457812028831800976635661652329037222471941230294013238317959082266249430008679265182723643180809288262932895869396508351055714991898917541169028643543990949433123262122354898265312371026754022483973748727117812188427415300671791170317742313481611737969715263637866694542505962058683112422533312540577202423610913237551319659210478098947317846535681791466791381032995356137064211874863411089949804324340551347666331158490106341364754424839883017164285207895629408930608197975300404191137792029542292558226619778190502998307628676701706701345351469020463930419169880309660278785077464297237450611557117054981156945940793582914964597385312914615523480643933885791320157896914180543328328415434986281583466299489112747642263362369596248791368597577401471193160992122176918746203416478616340722769873612803941948090591641262752006537035033638897367954661618165205610778189977205074187305019087735736065156254092470146228115918078830827262440737534047949495970550613303110954646810440955290786311152224496902981166532226390208472471687227986533628184648335621707450980470802433225174717702518851728702988600222432190791869970959014896231630760368626311110872339335132561795043198967452340764268329083145328500042990972022212684370220362853190319330785510147910974098218932069831049845694545035487124187395704667509095591366519266626782550690107586658661170778168998407786442811697154922957674559358435572162177058293474685876491959559917736829877905727796...
(√φ) = 1.272019649514069.
(√(2/((√(5) subtract 1)))) = 1.272019649514069:
https://www.scientificlib.com/en/Mathematics/Geometry/KeplerTriangle.html
https://www.wolframalpha.com/input?i=%28%E2%88%9A%CF%86%29
Minimal polynomial: x4 - x2 – 1:
https://www.wolframalpha.com/input?i=x%5E4+-+x%5E2+-+1
The square root of the Golden ratio = (√φ) = 1.272019649514069 to 1 million decimal places:
https://www.wolframalpha.com/input?i=%28%E2%88%9A%CF%86%29++to+1000000+decimal+places
sqrt(1/2 + sqrt(5)/2)
Many digits of the square root of the square root of the Golden ratio = (√√φ) =
1.12783848556168226026483548317704245843646833542365576729004918640047620953955361240399610929339306725461109156752945276596408294578932534109270337445638810775298145182487524623133012388077724863383651021399290676340599377801873312674975338384838753063450556762603008959823217968013676271799531731540040814584231972988772607605914051866268480992784605558969089031648366996136999943811531017391591284828318629174208291918071703269781438952961629302968550511604762160009907917109652565373357896285455147559030260549932563781680245239862364612835953818758462980442354928184370369614432097159698668811430433677451296748354676283213540620741452621063248633957427291819152141892913229550703659253658302452920417087752152388294477052953864870097865900079026736969798326233717141027913456035817163891530728319338341753225032897811092258691525782537234325716942547497858995626647277044412520224319601590514357970329494821334766348976963958585086098256660661695286974399865897701048779460083533098737383968700170584705126014603798182434389105449877987990654840589522982303546198130285465146350181292886985144094538949869596055515638086357025873063021752551592610611042094518186906289099858413746455232481505115197103625969802160277339153823671472230174545870882878196979928339606008763623164329800431089312327416793476276288019158646369240450958856017522306647605475800715837498132443103686308208261395177582135376540825782156056001881764120557087249638108195891176688405082704468133313723323637094448381396725175434973613643708811530810038033360228851388209193838156504634750506564711194165645555398018956864417497785950611633179476151071174294756181733558840445216121205834311746620794307919338260226492827949225461384077534610088069434843834314967684080506874910748862792879467478393366720222742900533872456472988890137049349840001824666486153005061300149995447721140842403342022775657874895639952311724943150574313150172712247664045245189799104629952306545419227245943819992124620098706223248636197644407916317733704638263710658128965905898112338805286861681396509247420516172160796787148754259684032836200378090756175670698582721411199021519881756717719235076603370906548242814648427151865860276576567417076218865922601067678452221049545437927091070115680093847631846346923787651211365923390455483269373863989814585349866507179286983757394256068062776119515311771847248143038051794790497199640451294091333073999546716712399701840821864620476678068371923404671759925734258065948277854409390860626441984353987540199809554935413560052255678228488089131219705101668401099788687828129675547736923637343777163753755266847268806983503555538998799179351309422002350888588438955153909070113613449685946787177602608911413719742613299165119643802609990489550275010345343419686811472819614754994571364855556318997013680213892013188825610619231569236827455843102073649685826516983367009029695159657819409408151160517662678474401155552088922283323156455187580655812764270174835566213343703263950198226435281691138195651795181586674114871601282640376436005610525547873891588606205456775504515458025377825761668733866103509739663103790512020683830494433786582130351744712579551378076306479327576730494008564130378320463546456354786064191544813372581927183643899740496375038154643394128404144413311244482693321884738063475280137697826144596539207477390435763010212458782281742306909375518794040236531336705345978008696808549601908452085978935249553233316393572562910875657071666309257643861376758034893670085543792626183962512326321168787943884432920312322471644649811351846424880170419552152382735711557378612227944364330299337184093991184624701537629795631305994821860926433669774061906602143851218215762788326885225361389078907427948984296998055580883349632261420101876749074163546699249895675579789985400351429035627559891581203372119989331256188468179338252641287886663479558760042412786144582623190221342370310181863552926099566695850919638479245885035530162880877774078841936698002339803183563614367246097327247874920183936348043225614574810339068983018794664221532631072305174937089184646066232766499600412333775081388250001984908187491919412858116616758346303553252233930...
(√√φ) = 1.127838485561682.
(√(√(2/((√(5) subtract 1))))) = 1.127838485561682.
https://www.wolframalpha.com/input?i=%28%E2%88%9A%E2%88%9A%CF%86%29
Minimal polynomial: x8 - x4 – 1:
https://www.wolframalpha.com/input?i=x%5E8+-+x%5E4+-+1
The square root of the square root of the Golden ratio = (√√φ) = 1.127838485561682 to 1 million decimal places:
https://www.wolframalpha.com/input?i=%28%E2%88%9A%E2%88%9A%CF%86%29+to+1000000+decimal+places
The 100% correct and exact value of 𝝿 = Pi = (4/√(2/((√(5) subtract 1)))) = 3.144605511029693144.
True value of 𝝿 = Pi = 4 divided by the square root of Phi = 1.618033988749895 = √φ = 1.272019649514069 = 3.144605511029693144.
𝝿 = Pi = (4/√(2/((√(5) subtract 1)))) = 3.144605511029693144.
3.144605511, π
4/(PHI ^ (1/2)) 4/√φ.
4/√(cosine (36 degrees) times 2)
4/√(sin (54 degrees) times 2)
(63245986/39088169) = (φ) = 1.618033988749895.
4/√(63245986/39088169) = 3.144605511029693144.
4/√((√(5) plus 1)/2) = 3.144605511029693144.
𝝿 = Pi = 4/√φ = 3.144605511029693144.
https://www.wolframalpha.com/input/?i=4%2F√φ
Minimal polynomial: x4 + 16x2 – 256 = 0
https://www.wolframalpha.com/input/?i=x4+%2B+16x2+%E2%80%93+256+%3D+0
Many digits of the true value of 𝝿 = Pi = 4/√φ =
3.14460551102969314427823434337183571809248823135089295065960788040472819048924365484765155663403254225951604897657844522350184148188477210145800112384535316599699631239446143308956024472240138513731315019765132501688867186247037873133594349618276234248844199296961553849723700557383552234689074536416980142043696409438174632694537726633954143989037097479242491578892978023339064417670841722688275153805921739970264230238511942422440819926855734374996579879446112389110161075513872073582816575721818832835163361391590239923536946900248451700445169927819854537616603505197208007189706440714096687578284372466332190268223400254077253538215266379226703698539085476164524369219532321073310447355259498023116536602160672047637738097925925582348768010853511874693389527014064437815680483743106640772234041399523439171855628610662401759766693576457654807513114186979169507365131852819274263669789734848841467364682016630510358289683679400824422762107807858027702527907929219431262826080982197730614327502037698328087258652874989125816265811400097484019434115778437762432062885283659544778783918439235015209646583302138065336812477045456661566501765205387450234265373372161991167980365463100808493531941916284776011418422257191272998016027019002493897205974866800395517157330654521192827101984095193986604557708773526988266135536640269714447913210489977552594544514535924331665830961478322636156141381547256570914886171308690084360521911131332231286516085214835390759402196975165837478624908096417779086760927814627162297202858370814646941921393469849993344827687062794497441030872679661684753940658343549695027014970131695954965403173384776717870110087068501942344201049850605832313078203557299262308991531932281983738305755168635692254905747555234188780153475673339525234292355702483261692142651508173990671264350154250362859075548008747566672616205028820240543741715414546972253736859789971028216629678873571789763181141705324833731834927057821859523945472696974792741640618435301751030640565228206985544741052203284577140924150594729813002144044112763823306139041380300126396086798057969386101655998320393440566528706918145904700851594664062268446171800960535273637429591695113304810670181928845223783455842698791632288933712236058964642712732019149724711033642439113411406279984988240202336986202113294499550017764047395624978771400686498011825833359728093789411972989450893540930512941375411293556882777422642065983017517841947188657568092066411253628272642711179961093309021746733833999601981997280412551129615031389594123251078882807792913953451339014143977331590194423675330330534577756269776382209443582858953273327176324990580032792293533438613176525658218413317372453292985834019389688763668570542857298926750775038077114605826312310376399709687611339396644421253988853854789904729935753699004476840608807945167967305710691731329019095129076568042197176427501094156863714829572955183146968025073021442840734279027927090460158641969824821979818744940365983424234313031337087076473104153434653637954742233815350483225369099430166060429532277020206218783146105484227853209504583393891454212649046699400421908425470505305991165172689865132188157173588974197397975288180670698818541011798133792272762021101366593963233743826713623469749078052664159747967223554289772947860425599027490096547502797993195877230189445672756690096861461070693330814888966007259565666724589310401040986830914782601333930577391752551112385849125356976936458893882824135239978458650854478402921241124531624714291678469084458329421240510389886417994318274412611981844172248963848516145523706771809405744385793916822895294232088845607432701878054161586964652586926326767438873383064488676319971374949250207775636350660819838082934235612496822389803904407009527313363755526274289810347679119254762151567013910590191327466184437856992286688720925715020198926545387089270653710334302796513610228588001990985835649506857882226324949103678172164225422584290507043642062125182690961507926947618787148829059027709825067815383429199238478946359301782419137009781956771137312270657985475230369802641927217001863249724276906966227235524987009401778481285814707840895854213203788218923365891705920...
The correct value of 𝝿 = Pi = 4/√φ = 3.144605511029693144.
(15 decimal places). 𝝿 = Pi = 4/√φ = 3.144605511029693.
(18 decimal places). 𝝿 = Pi = 4/√φ = 3.144605511029693144.
(50 decimal places) 𝝿 = Pi = 4/√φ = 3.14460551102969314427823434337183571809248823135089
(60 decimal places) 𝝿 = Pi = 4/√φ = 3.14460551102969314427823434337183571809248823135089295065961
The true value of 𝝿 = 4/√φ = 3.144605511029693144 to 1million decimal places:
https://www.wolframalpha.com/input?i=4%2F%E2%88%9A%CF%86+to+1000000+decimal+places
Pi = 3.144 #198:
https://www.youtube.com/watch?v=asJ1xDh4UfU
The Real number pi on facebook:
https://m.facebook.com/TheRealNumberPi/
Traditional 𝝿 = Pi = 51066975/16255123 = 3.141592653589793 is false.
Traditional 𝝿 = Pi = (10 ^ 12)/(16255123/10213395)/(2)/(10 ^ 11) = 3.141592653589793 is false.
Traditional 𝝿 = Pi = ((10 ^ 42)/(30685681/9640191)) = 3.141592653589793 is false.
Traditional 𝝿 = Pi = (4/√(48908982/30169519)) = 3.141592653589793 is false.
The true value of 𝝿 = Pi = 4/√φ = 3.144605511029693144:
http://www.measuringpisquaringphi.com/